Média Móvel

O que é uma média móvel?

Uma média móvel é um indicador gráfico utilizado para suavizar as variações em determinado conjunto de dados. Ela também pode ser utilizada como um indicador de tendência ou de zonas de suporte e resistência.

Suponha que você tenha, por exemplo, o gráfico do preço de uma ação ao longo do tempo.

Devido às variações aleatórias do preço, pode ser difícil identificar uma tendência no gráfico (figura 1).

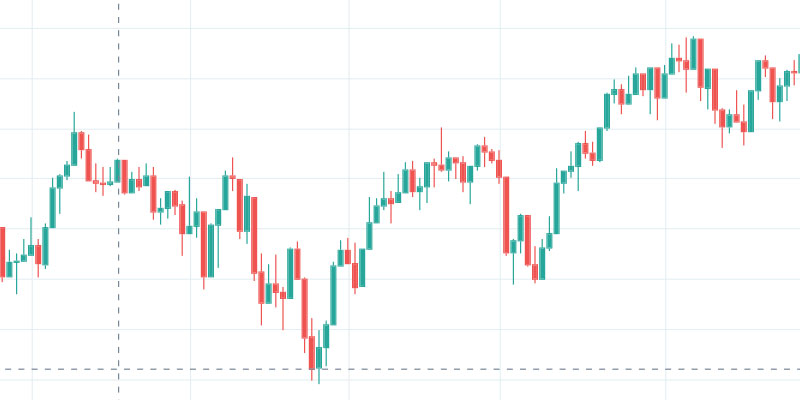
Média Móvel

Figura 1 - Gráfico do IBOVESPA. Fonte: tradingview.com.

Utilizando uma média móvel, é possível suavizar as variações e observar com mais clareza a tendência de movimento dos preços (figura 2).

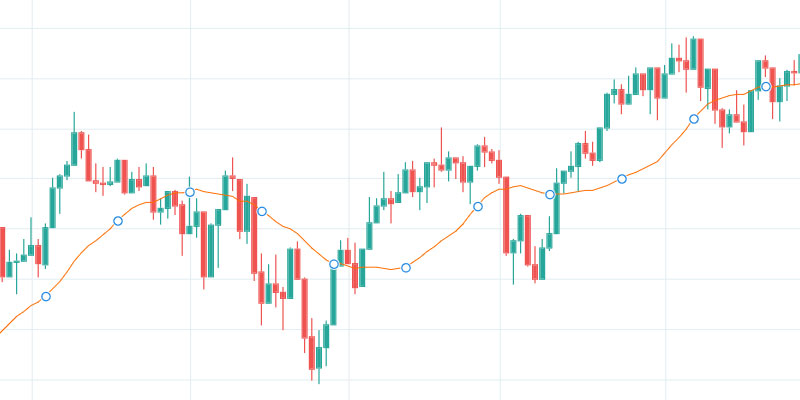
Média Móvel

Figura 2 - Gráfico do IBOVESPA com média móvel simples de 22 dias (linha laranja). Fonte: tradingview.com.

Existem diversas formas de se calcular média móveis, mas as mais comuns são:

  • Média Móvel Simples; e
  • Média Móvel Exponencial.

Média Móvel Simples

Para calcular uma média móvel simples:

  1. Escolha um período de tempo (n);
  2. Some os primeiros n dados disponíveis;
  3. Divida o resultado de 2 por n.
  4. A partir dái, elimine o dados mais antigo e some o dado mais novo; e
  5. Divida o resultado por n.

$$ MMS = {{D {\tiny 1} + D {\tiny 2} + + D {\tiny 3} + ...} \over n } $$

Fórmula 1 - Cálculo da Média Móvel Simples.

Por exemplo, suponha que você tenha o seguinte grupo de dados:


5, 7, 8, 10, 6, 2, 10, 12, 15, 18, 20, 17, 26,
22, 18, 16, 15, 19, 24, 27, 28, 29 e 30.
Exemplo de dados.

Vamos calcula a média móvel de 5 períodos para esse grupo de dados:

Começamos por somar os 5 primeiros dados disponíveis:

$$ 5 + 7 + 8 + 10 + 6 = 36 $$

Passo 1: somar os dados conforme o período desejado.

Em seguida, dividimos pelo número de períodos:

$$ MMS = { 36 \over 5 } = 7,2 $$

Passo 2: dividir os dados pelo período desejado.

Para obter o próximo valor da média, excluímos o dado mais antigo e inserimos o dado novo:

$$ MMS = {\bcancel{5} + 7 + 8 + 10 + 6 + \boxed{2} \over 5} = { 33 \over 5} = 6,6 $$

Passo 3: recalcular retirando-se o dado mais antigo e inserindo-se o próximo valor.

A partir daí, repetimos o processo para os demais dados.

Dados MMS
5
7
8
10
6 7,20
2 6,60
10 7,20
12 8,00
15 9,00
18 11,40
20 15,00
17 16,40
26 19,20
22 20,60
18 20,60
16 19,80
15 19,40
19 18,00
24 18,40
27 20,20
28 22,60
29 25,40
30 27,60
Figura 3 - Exemplo de cálculo de de média móvel simples de período 5.

Média Móvel Exponencial

A média móvel exponencial (MME) dá um peso maior para valores mais recentes.

Para calcular a MME:

  1. Calcule a média móvel simples de período n;
  2. Calcule o fator multiplicador (fórmula 2); e
  3. Utilize a fórmula da MME para calcular o valor (fórmula 3).

$$ fator = {2 \over {n + 1}} $$

Fórmula 2 - Cálculo do fator de ajuste da Média Móvel Exponencial.

$$ EMA = {(D {\tiny 1} - EMA {\tiny o}) \times fator + EMA {\tiny o}} $$

Fórmula 3 - Cálculo da Média Móvel Exponencial.

Onde:

  • D1 = dado mais recente; e
  • EMAo = EMA anterior.

Por exemplo, suponha que você tenha o seguinte grupo de dados:


5, 7, 8, 10, 6, 2, 10, 12, 15, 18, 20, 17, 26,
22, 18, 16, 15, 19, 24, 27, 28, 29 e 30.
Exemplo de dados.

Vamos calcular a MME para o período de 5.

Inicialmente, calcule a MMS dos primeiros 5 dados:

$$ MMS = {5 + 7 + 8 + 10 + 6 \over 5} = { 36 \over 5} = 7,2 $$

Passo 1: calcular a média simples conforme o período desejado.

A primeira EMA, será igual a MMS.

Calculamos, então, o fator de ajuste:

$$ fator = {2 \over (5 + 1)} = 0,33 $$

Passo 2: calcular o fator de ajuste.

Em seguida, calculamos a EMA para o próximo dado (2):

$$ EMA = {(2 - 7,2) \times 0,33 + 7,2 } = 5,47 $$

Passo 3: calcular o próximo valor.

A partir daí, repetimos o processo para os demais dados:

Dados Fator MME
5
7
8
10
6 0,33 7,20
2 0,33 5,47
10 0,33 8,11
12 0,33 8,50
15 0,33 10,17
18 0,33 11,61
20 0,33 14,20
17 0,33 15,93
26 0,33 19,76
22 0,33 19,95
18 0,33 19,95
16 0,33 19,28
15 0,33 18,37
19 0,33 19,61
24 0,33 19,46
27 0,33 20,91
28 0,33 22,56
29 0,33 24,75
30 0,33 27,15
Figura 3 - Exemplo de cálculo de de média móvel exponencial de período 5.

Simples e Exponencial

Enquanto a a média móvel exponencial (MME) dá um peso maior para valores mais recentes, a média móvel simples (MMS) dá o mesmo peso para todos os valores.

Isso faz com que a MME seja mais sensível as variações recentes nos dados, tornando-se menos "atrasada" do que MMS.

A escolha por um tipo ou outro dependerá do analista e de sua preferência.

Média Móvel

Figura 4 - Gráfico do IBOVESPA com média móvel simples de 22 dias (linha laranja) e média móvel exponecial de 22 dias (linha azul). Observe como a MME responde mais rápido às variações no preço. Fonte: tradingview.com.

Período

Pode ser utilizado qualquer período para o cálculo da média móvel.

A escolha por determinado período dependerá da preferência do analista.

Os períodos mais utilizados para gráficos diários de preço são:

  • 9: para tendências de curto prazo;
  • 22: para tendências de médio prazo; e
  • 200: para tendências de longo prazo.

Quanto maior for o período selecionado, mais suave será a curva formada pelos valores da média móvel.